[“Constrained Diffusion Decomposition”]

An example is available.

Use git clone

git clone https://github.com/gxli/Constrained-Diffusion-Decomposition.git
cd constrained_diffusion
pip install .

Use pip

pip install --upgrade scipy numpy 
pip install -i https://test.pypi.org/simple/ constrained-diffusion==1.0.1   

https://test.pypi.org/project/constrained-diffusion/1.0.1/

numpy nd array, of shape e.g. (nx, ny, nz).

result: numpy nd array, of shape (m, nx, ny, nz). The mth commponent contain structures of sizes 2$^(m-1)$ to 2$^m$ pixels.

residual: numpy nd array, of shape (nx, ny, nz) the input data will be recovered as input = sum_i result[i] + residual.

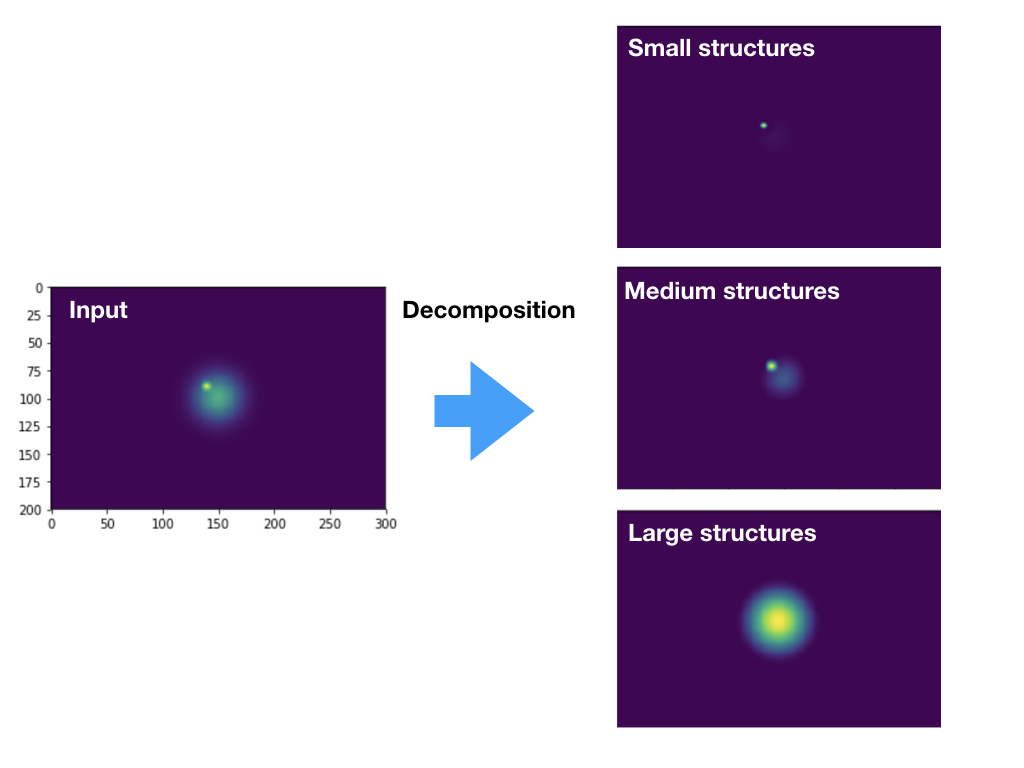
For example

More examples

import constrained_diffusion as cdd

result, residual = cdd.constrained_diffusion_decomposition(data)

Assuuming an input of I(x, y),t he decomposition is achieved by solving the equation

    \frac{\partial I_t }{\partial t} ={\rm sgn}(I_t) \mathcal{H}({- \rm sgn}(I_t) \nabla^2 I_t) \nabla^2 I_t

where t is related to the scale l by t = l**2.